Cuando Henrrieta Leavitt en 1912, presentó su artículo sobre las cefeidas en donde proponía una ley, que después sería llamada: la ley de Leavitt. Utilizó una herramienta matemática llamada regresión lineal, o en términos un poco más vulgares: hizo un ajuste lineal a sus datos observacionales. Aquí pretendemos adentrarnos en dicha herramienta.
Un ajuste lineal es una herramienta de predicción, en la que se pretende, partiendo de una cierta cantidad de datos, obtener un modelo matemático, el cual por medio de una ecuación represente lo más fielmente posible el comportamiento futuro de dichos datos. Lo que pretendemos al hacer el ajuste es, llenar de rigor matemático a posibles sucesos, haciendo uso de métodos estadísticos. Conociendo sucesos ya ocurridos: los datos.
Para entender mejor la herramienta, usaremos un conjunto de datos, y junto con un programa realizado en Python, haremos un ajuste lineal. Ambos archivos los puedes encontrar debajo de la entrada para que los uses a tu antojo. En la imagen vemos una parte de los datos a ajustar, tenemos niveles de glucosa contra dosis requeridas de insulina en una muestra de mujeres. Podemos representar cualesquiera datos que obtengamos por medio de experimentos u observaciones como puntos en una gráfica como la observada a continuación.
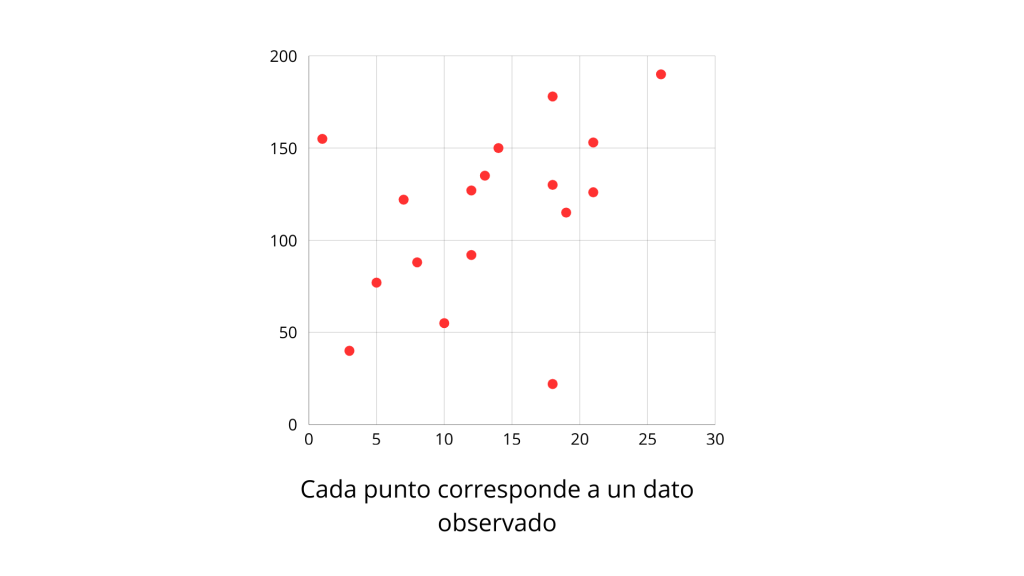
Nos interesa particularmente una tendencia lineal, dicha situación se observa cuando existe una relación clara entre variables y tiende a aumentar a medida que lo hace x. De hecho, si pusiéramos una regla e intentáramos trazar una línea que pase por todos los puntos veríamos, la tendencia lineal. Esa es la idea general detrás del ajuste lineal. Encontrar esa línea que se ajuste mejor a todos los puntos.
Escribiremos la ecuación de una línea recta de la siguiente forma:
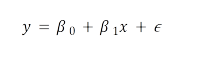
Donde el primer termino con el subindice 0, beta, es la intersección con el eje y, y beta con el subindice 1 es la pendiente, el elemento nuevo agregado, ε es el responsable del ajuste. ε es una variable aleatoria con valor esperado igual a 0, vamos a hacer también, la suposición que para dos valores i y j corresponderá a las observaciones yi, yj respectivamente con ij. Esto significa el promedio de y se encuentra relacionado linealmente con x y que tiene una desviación hacia abajo o hacia arriba de la recta sugerida. Como en la imagen en la que es la barra de desviación con respecto a la recta.
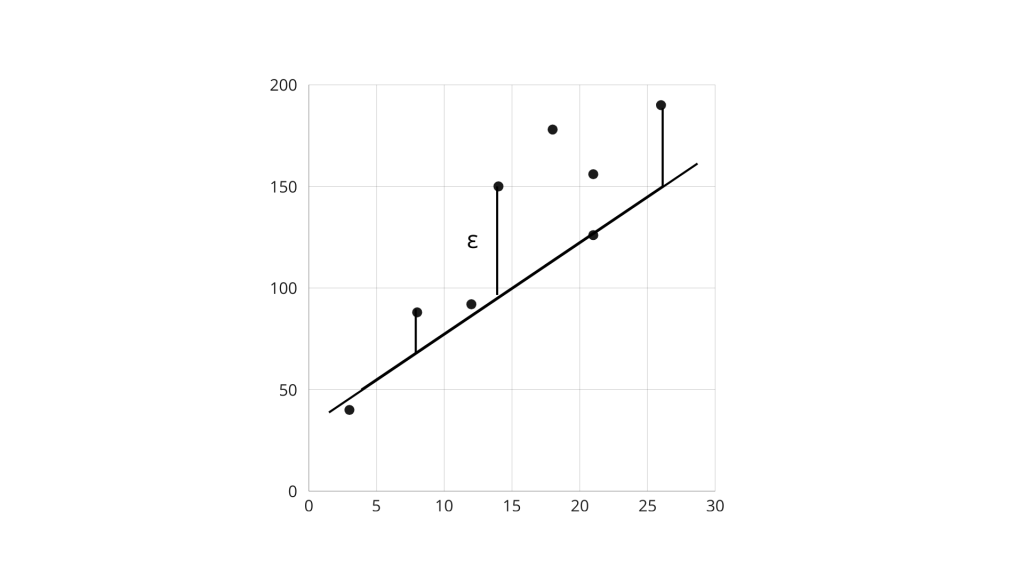
¿Cómo hacemos el ajuste? El método teórico usado es el conocido como mínimo cuadrados (existen distintas formas de hacer ajustes lineales, pero este es una de los más usados) el cual consiste en que: “se toma la recta de mejor ajuste aquella que minimiza la suma de los cuadrados de las desviaciones de los valores observados de y” (Mendenhal, 1979, Introducción a la probabilidad y la estadística) lo que nos quiere decir la cita anterior es que debemos encontrar numéricamente los valores de las β, para encontrar de esa manera la ecuación que mejor describe los datos estadísticos. Hacer estimaciones de la pendiente y de la intersección con el eje y. Las ecuaciones que describen el método son tal como su nombre lo dice, sumas de cuadrados, y son las siguientes:

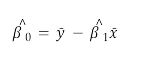
donde:


La ecuación encontrada que ajusta los datos, correspondiente al grafico de Insulina contra la Glucosa:
y=2.24x−118.64
La pendiente de nuestro ajuste es 2.24, esto es, la inclinación de la recta y se corta la misma en el eje y en el punto -118.64.
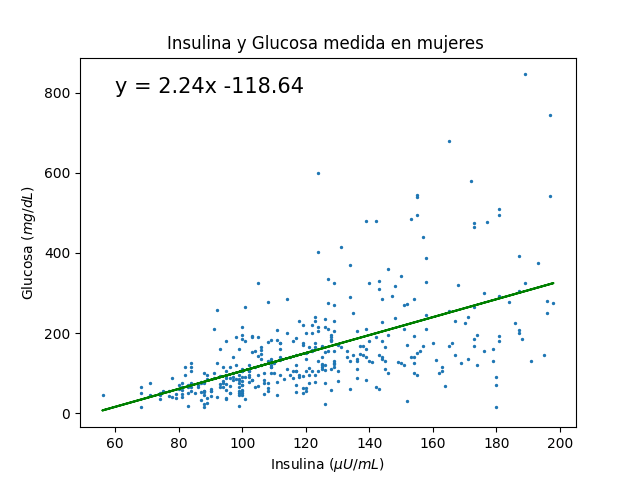
Intencionalmente usamos un conjunto de datos en donde cuya relación sea clara, todos entendemos que si se nos sube el azúcar necesitamos aumentar la dosis de insulina.
El siguiente código escrito con Python 3, realiza un ajuste lineal a un conjunto de datos de un grupo de mujeres. El código hace el ajuste y grafica los puntos que corresponde a los datos así como a la recta que mejor se ajusta.
import matplotlib.pyplot as plt
import csv
def fit1(x,y):
k = 0
for i,j in zip(x,y):
k = i * j + k
return k
def fit2(x,y):
k = 0
l = 0
for i,j in zip(x,y):
k = k + i
l = l + j
return k * l
def fit3(x):
k = 0
for i in x:
k = k + i ** 2
return k
def fit4(x):
k = 0
for i in x:
k = k + i
return k ** 2
def fit(x,y):
if len(x) == len(y):
a1 = fit1(x, y)
a2 = fit2(x, y)
a3 = fit3(x)
a4 = fit4(x)
return a1, a2, a3, a4
def prom(z):
j = 0
for i in z:
j = j + i
return j / (len(z))
def equ(sum1, sum2, sum3, sum4, x, y):
n = len(x)
m = (n * sum1 - sum2) / (n * sum3 - sum4)
b = prom(y) - m * prom(x)
return m, b
def plot(m, b, x, xx):
y = []
for i in x:
y.append(b + m * i)
plt.scatter(x,xx, s= 2)
plt.plot(x, y, color = "green")
plt.xlabel(r"Insulina ($\mu U/mL$) ")
plt.ylabel(r"Glucosa ($mg/dL$)")
plt.title("Insulina y Glucosa medida en mujeres ")
plt.text(60,800, f'y = {m:.2f}x {b:.2f}', fontsize=15)
plt.show()
with open('diabetes.csv', newline='') as csvfile:
spamreader = csv.reader(csvfile, delimiter=',', quotechar='|')
data = []
data2 = []
for row in spamreader:
data.append(float(row[1]))
data2.append(float(row[4]))
data1_2 = [x for x, y in zip(data, data2) if y != 0]
data2_2 = [y for y in data2 if y != 0]
data1_22 = [d for d in data1_2 if d != 0]
data2_22 = [d2 for d, d2 in zip(data1_2, data2_2) if d != 0]
a1, a2, a3, a4 = fit(data1_22, data2_22)
m, b = equ(a1, a2, a3, a4, data1_22, data2_22)
plot(m, b, data1_22, data2_22)Referencia del Dataset:
Satre, Sakshi (2024). Female Diabetes Dataset. Focusing on women’s Well-being: Investigating Diabetes Trends. Kaggle. http://www.kaggle.com/datasets/sakshisatre/female-diabetes-dataset/data

Deja un comentario